第 7 章 DQN 算法
7.1 简介
在第 5 章讲解的 Q-learning 算法中,我们以矩阵的方式建立了一张存储每个状态下所有动作
对于这种情况,我们需要用函数拟合的方法来估计
7.2 CartPole 环境
以图 7-1 中所示的所示的车杆(CartPole)环境为例,它的状态值就是连续的,动作值是离散的。

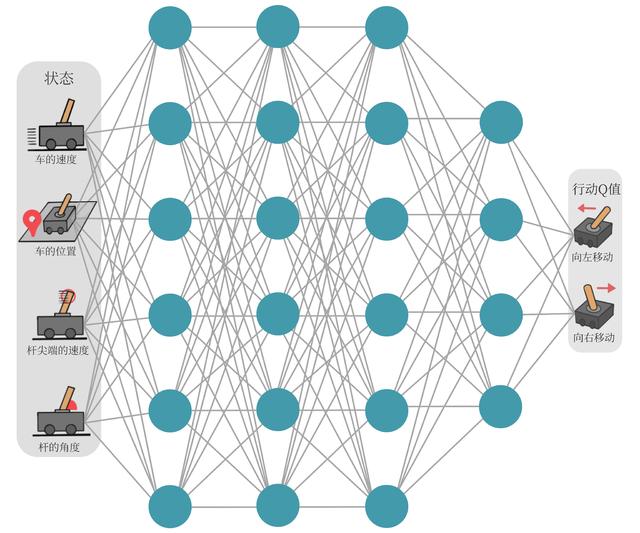
在车杆环境中,有一辆小车,智能体的任务是通过左右移动保持车上的杆竖直,若杆的倾斜度数过大,或者车子离初始位置左右的偏离程度过大,或者坚持时间到达 200 帧,则游戏结束。智能体的状态是一个维数为 4 的向量,每一维都是连续的,其动作是离散的,动作空间大小为 2,详情参见表 7-1 和表 7-2。在游戏中每坚持一帧,智能体能获得分数为 1 的奖励,坚持时间越长,则最后的分数越高,坚持 200 帧即可获得最高的分数。
| 维度 | 意义 | 最小值 | 最大值 |
|---|---|---|---|
| 0 | 车的位置 | -2.4 | 2.4 |
| 1 | 车的速度 | -Inf | Inf |
| 2 | 杆的角度 | ~ -41.8° | ~ 41.8° |
| 3 | 杆尖端的速度 | -Inf | Inf |
| 标号 | 动作 |
|---|---|
| 0 | 向左移动小车 |
| 1 | 向右移动小车 |
7.3 DQN
现在我们想在类似车杆的环境中得到动作价值函数
那么 Q 网络的损失函数是什么呢?我们先来回顾一下 Q-learning 的更新规则(参见 5.5 节):
上述公式用时序差分(temporal difference,TD)学习目标
至此,我们就可以将 Q-learning 扩展到神经网络形式——深度 Q 网络(deep Q network,DQN)算法。由于 DQN 是离线策略算法,因此我们在收集数据的时候可以使用一个
7.3.1 经验回放
在一般的有监督学习中,假设训练数据是独立同分布的,我们每次训练神经网络的时候从训练数据中随机采样一个或若干个数据来进行梯度下降,随着学习的不断进行,每一个训练数据会被使用多次。在原来的 Q-learning 算法中,每一个数据只会用来更新一次
(1)使样本满足独立假设。在 MDP 中交互采样得到的数据本身不满足独立假设,因为这一时刻的状态和上一时刻的状态有关。非独立同分布的数据对训练神经网络有很大的影响,会使神经网络拟合到最近训练的数据上。采用经验回放可以打破样本之间的相关性,让其满足独立假设。
(2)提高样本效率。每一个样本可以被使用多次,十分适合深度神经网络的梯度学习。
7.3.2 目标网络
DQN 算法最终更新的目标是让
(1)原来的训练网络
(2) 目标网络
综上所述,DQN 算法的具体流程如下:
- 用随机的网络参数
初始化网络 - 复制相同的参数
来初始化目标网络 - 初始化经验回放池
- for 序列
do 获取环境初始状态 for 时间步 do 根据当前网络 以 -贪婪策略选择动作 执行动作 ,获得回报 ,环境状态变为 将 存储进回放池 中 若 中数据足够,从 中采样 个数据 对每个数据,用目标网络计算 最小化目标损失 ,以此更新当前网络 更新目标网络 end for - end for
7.4 DQN 代码实践
接下来,我们就正式进入 DQN 算法的代码实践环节。我们采用的测试环境是 CartPole-v0,其状态空间相对简单,只有 4 个变量,因此网络结构的设计也相对简单:采用一层 128 个神经元的全连接并以 ReLU 作为激活函数。当遇到更复杂的诸如以图像作为输入的环境时,我们可以考虑采用深度卷积神经网络。
从 DQN 算法开始,我们将会用到rl_utils库,它包含一些专门为本书准备的函数,如绘制移动平均曲线、计算优势函数等,不同的算法可以一起使用这些函数。为了能够调用rl_utils库,请从本书的GitHub 仓库下载rl_utils.py文件。
import randomimport gymimport numpy as npimport collectionsfrom tqdm import tqdmimport torchimport torch.nn.functional as Fimport matplotlib.pyplot as pltimport rl_utils
首先定义经验回放池的类,主要包括加入数据、采样数据两大函数。
class ReplayBuffer:''' 经验回放池 '''def __init__(self, capacity):self.buffer = collections.deque(maxlen=capacity) # 队列,先进先出def add(self, state, action, reward, next_state, done): # 将数据加入bufferself.buffer.append((state, action, reward, next_state, done))def sample(self, batch_size): # 从buffer中采样数据,数量为batch_sizetransitions = random.sample(self.buffer, batch_size)state, action, reward, next_state, done = zip(*transitions)return np.array(state), action, reward, np.array(next_state), donedef size(self): # 目前buffer中数据的数量return len(self.buffer)
然后定义一个只有一层隐藏层的 Q 网络。
class Qnet(torch.nn.Module):''' 只有一层隐藏层的Q网络 '''def __init__(self, state_dim, hidden_dim, action_dim):super(Qnet, self).__init__()self.fc1 = torch.nn.Linear(state_dim, hidden_dim)self.fc2 = torch.nn.Linear(hidden_dim, action_dim)def forward(self, x):x = F.relu(self.fc1(x)) # 隐藏层使用ReLU激活函数return self.fc2(x)
有了这些基本组件之后,接来下开始实现 DQN 算法。
class DQN:''' DQN算法 '''def __init__(self, state_dim, hidden_dim, action_dim, learning_rate, gamma,epsilon, target_update, device):self.action_dim = action_dimself.q_net = Qnet(state_dim, hidden_dim,self.action_dim).to(device) # Q网络# 目标网络self.target_q_net = Qnet(state_dim, hidden_dim,self.action_dim).to(device)# 使用Adam优化器self.optimizer = torch.optim.Adam(self.q_net.parameters(),lr=learning_rate)self.gamma = gamma # 折扣因子self.epsilon = epsilon # epsilon-贪婪策略self.target_update = target_update # 目标网络更新频率self.count = 0 # 计数器,记录更新次数self.device = devicedef take_action(self, state): # epsilon-贪婪策略采取动作if np.random.random() < self.epsilon:action = np.random.randint(self.action_dim)else:state = torch.tensor([state], dtype=torch.float).to(self.device)action = self.q_net(state).argmax().item()return actiondef update(self, transition_dict):states = torch.tensor(transition_dict['states'],dtype=torch.float).to(self.device)actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(self.device)rewards = torch.tensor(transition_dict['rewards'],dtype=torch.float).view(-1, 1).to(self.device)next_states = torch.tensor(transition_dict['next_states'],dtype=torch.float).to(self.device)dones = torch.tensor(transition_dict['dones'],dtype=torch.float).view(-1, 1).to(self.device)q_values = self.q_net(states).gather(1, actions) # Q值# 下个状态的最大Q值max_next_q_values = self.target_q_net(next_states).max(1)[0].view(-1, 1)q_targets = rewards + self.gamma * max_next_q_values * (1 - dones) # TD误差目标dqn_loss = torch.mean(F.mse_loss(q_values, q_targets)) # 均方误差损失函数self.optimizer.zero_grad() # PyTorch中默认梯度会累积,这里需要显式将梯度置为0dqn_loss.backward() # 反向传播更新参数self.optimizer.step()if self.count % self.target_update == 0:self.target_q_net.load_state_dict(self.q_net.state_dict()) # 更新目标网络self.count += 1
一切准备就绪,开始训练并查看结果。我们之后会将这一训练过程包装进rl_utils库中,方便之后要学习的算法的代码实现。
lr = 2e-3num_episodes = 500hidden_dim = 128gamma = 0.98epsilon = 0.01target_update = 10buffer_size = 10000minimal_size = 500batch_size = 64device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")env_name = 'CartPole-v0'env = gym.make(env_name)random.seed(0)np.random.seed(0)env.seed(0)torch.manual_seed(0)replay_buffer = ReplayBuffer(buffer_size)state_dim = env.observation_space.shape[0]action_dim = env.action_space.nagent = DQN(state_dim, hidden_dim, action_dim, lr, gamma, epsilon,target_update, device)return_list = []for i in range(10):with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:for i_episode in range(int(num_episodes / 10)):episode_return = 0state = env.reset()done = Falsewhile not done:action = agent.take_action(state)next_state, reward, done, _ = env.step(action)replay_buffer.add(state, action, reward, next_state, done)state = next_stateepisode_return += reward# 当buffer数据的数量超过一定值后,才进行Q网络训练if replay_buffer.size() > minimal_size:b_s, b_a, b_r, b_ns, b_d = replay_buffer.sample(batch_size)transition_dict = {'states': b_s,'actions': b_a,'next_states': b_ns,'rewards': b_r,'dones': b_d}agent.update(transition_dict)return_list.append(episode_return)if (i_episode + 1) % 10 == 0:pbar.set_postfix({'episode':'%d' % (num_episodes / 10 * i + i_episode + 1),'return':'%.3f' % np.mean(return_list[-10:])})pbar.update(1)
Iteration 0: 100%|██████████████████████████████████████████| 50/50 [00:00<00:00, 589.55it/s, episode=50, return=9.300]Iteration 1: 100%|█████████████████████████████████████████| 50/50 [00:00<00:00, 60.01it/s, episode=100, return=12.300]Iteration 2: 100%|████████████████████████████████████████| 50/50 [00:04<00:00, 11.94it/s, episode=150, return=123.000]Iteration 3: 100%|████████████████████████████████████████| 50/50 [00:15<00:00, 3.27it/s, episode=200, return=159.300]Iteration 4: 100%|████████████████████████████████████████| 50/50 [00:16<00:00, 3.04it/s, episode=250, return=192.200]Iteration 5: 100%|████████████████████████████████████████| 50/50 [00:15<00:00, 3.23it/s, episode=300, return=199.900]Iteration 6: 100%|████████████████████████████████████████| 50/50 [00:15<00:00, 3.28it/s, episode=350, return=193.400]Iteration 7: 100%|████████████████████████████████████████| 50/50 [00:16<00:00, 3.10it/s, episode=400, return=200.000]Iteration 8: 100%|████████████████████████████████████████| 50/50 [00:15<00:00, 3.28it/s, episode=450, return=172.300]Iteration 9: 100%|████████████████████████████████████████| 50/50 [00:15<00:00, 3.32it/s, episode=500, return=185.000]
episodes_list = list(range(len(return_list)))plt.plot(episodes_list, return_list)plt.xlabel('Episodes')plt.ylabel('Returns')plt.title('DQN on {}'.format(env_name))plt.show()mv_return = rl_utils.moving_average(return_list, 9)plt.plot(episodes_list, mv_return)plt.xlabel('Episodes')plt.ylabel('Returns')plt.title('DQN on {}'.format(env_name))plt.show()


可以看到,DQN 的性能在 100 个序列后很快得到提升,最终收敛到策略的最优回报值 200。我们也可以看到,在 DQN 的性能得到提升后,它会持续出现一定程度的震荡,这主要是神经网络过拟合到一些局部经验数据后由
7.5 以图像为输入的 DQN 算法
在本书前面章节所述的强化学习环境中,我们都使用非图像的状态作为输入(例如车杆环境中车的坐标、速度),但是在一些视频游戏中,智能体并不能直接获取这些状态信息,而只能直接获取屏幕中的图像。要让智能体和人一样玩游戏,我们需要让智能体学会以图像作为状态时的决策。我们可以利用 7.4 节的 DQN 算法,将卷积层加入其网络结构以提取图像特征,最终实现以图像为输入的强化学习。以图像为输入的 DQN 算法的代码与 7.4 节的代码的不同之处主要在于 Q 网络的结构和数据输入。DQN 网络通常会将最近的几帧图像一起作为输入,从而感知环境的动态性。接下来我们实现以图像为输入的 DQN 算法,但由于代码需要运行较长的时间,我们在此便不展示训练结果。
class ConvolutionalQnet(torch.nn.Module):''' 加入卷积层的Q网络 '''def __init__(self, action_dim, in_channels=4):super(ConvolutionalQnet, self).__init__()self.conv1 = torch.nn.Conv2d(in_channels, 32, kernel_size=8, stride=4)self.conv2 = torch.nn.Conv2d(32, 64, kernel_size=4, stride=2)self.conv3 = torch.nn.Conv2d(64, 64, kernel_size=3, stride=1)self.fc4 = torch.nn.Linear(7 * 7 * 64, 512)self.head = torch.nn.Linear(512, action_dim)def forward(self, x):x = x / 255x = F.relu(self.conv1(x))x = F.relu(self.conv2(x))x = F.relu(self.conv3(x))x = F.relu(self.fc4(x))return self.head(x)
7.6 小结
本章讲解了 DQN 算法,其主要思想是用一个神经网络来表示最优策略的函数
7.7 参考文献
[1] VOLODYMYR M, KAVUKCUOGLU K, SILVER D, et al. Human-level control through deep reinforcement learning [J]. Nature, 2015, 518(7540): 529-533.
[2] VOLODYMYR M, KAVUKCUOGLU K, SILVER D, et al. Playing atari with deep reinforcement learning [C]//NIPS Deep Learning Workshop, 2013.